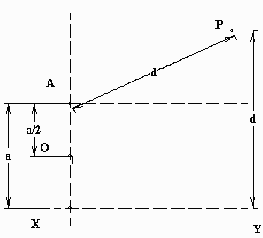
Apollonius is an interactive sketch-based geometry system that allows the user to sketch in some geometry and then define it precisely by specifying the dimensions. The above drawing is just a sketch; no dimensions have been imposed. In the next figure we have given three sides. When this is done the drawing snaps into the correct shape.
Apollonius keeps track of the dimensions and can detect redundant and inconsistent dimensions. This is a very powerful learning tool because the system can tell the student when they have the right information to define the geometry or when the information they have given is inconsistent.



In addition Apollonius can do graphing, tables, animation and has a formula calculator.



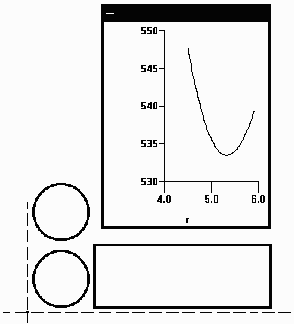
Below, we have illustrated an example from the NCTM Standards. A manufacturer, who has to design a cylindrical can to hold a specified volume, wishes to keep the area to a minimum. The area is the sum of the two circles and a rectangle. This is a common problem in a calculus course but the NCTM Standards recommend that such questions be investigated, using graphing and other computer technology, at a much earlier stage. I have seen elementary school students use Apollonius to study geometry and to solve problems that I do not believe they could have done without such software.
Apollonius can animate this situation and the student can practice his or her visual estimation skills. It is impossible to show the power of the animation in this document but the following diagram may give you an idea of what it is like.



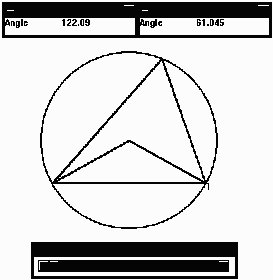
Apollonius is a very versatile exploratory tool for geometry and trigonometry. In the example below we are examining the property that the angle at the center of a circle is always twice that at the circumference when the two angles are on the same chord.
Unfortunately, the picture has not come out very well here. The black area below the circle is a scroll bar which allows the user to animate the figure, interactively changing any dimension and hence exploring the geometry. Above the circle are two small windows, one for each angle. As the student dynamically changes the geometry these two windows will continue to show the angles. These angles will, of course, change - but one will always be twice the other. This is a very powerful way for a student to become convinced of the underlying geometrical theorem.



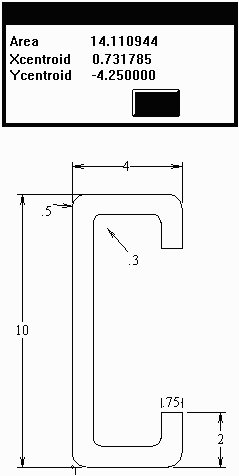
The student can interrogate the drawing for any of the standard geometrical properties. In the next figure we have drawn a C-section. Notice that this section includes the rounded corners. A simple inquiry gives the area (accurately taking into account the rounded corners) and the position of the centroid.
In order for Apollonius to so completely resolve all the geometry it, clearly, must have trigonometric capability. This capability is quite general and would be useful to the student studying trigonometric or circular functions, the basic trigonometric identities and the inverse trigonometric functions.
Recently, at Beaverton High School in Oregon, 90 students were using Apollonius to investigate the geometry of triangles, parallelograms, and circles and to do trigonometry. All this was done within the first class period and without any prior introduction to the software.



The possibilities are endless. Let me finish with just one more example. The visual, non-coordinate, definition of a parabola is the locus of points equidistant from a fixed point and a fixed line. This is very direct and simple to set up in Apollonius.



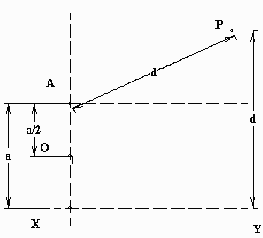
The point P is defined to be a distance d from the point A and t he same distance from the line XY. All we now need to do is to animate the value of "d" and P will trace a parabola.